6月26日
10.3 ポアソン回帰に対するメトロポリスアルゴリズム
現在値$\beta^{(s)}$と提案値$\beta^*$があるときのメトロポリスアルゴリズムによる受容率
\[\begin{align*} r &= \frac{p(\boldsymbol{\beta}^* \mid \mathbf{X}, \mathbf{y})}{p(\boldsymbol{\beta}^{(s)} \mid \mathbf{X}, \mathbf{y})}\\ &= \frac{\prod_{i=1}^{n} \mathrm{dpois}(y_i, \mathbf{x}_i^T \boldsymbol{\beta}^*)}{\prod_{i=1}^{n} \mathrm{dpois}(y_i, \mathbf{x}_i^T \boldsymbol{\beta}^{(s)})} \times \frac{\prod_{j=1}^{3} \mathrm{dnorm}(\beta_j^*, 0, 10)}{\prod_{j=1}^{3} \mathrm{dnorm}(\beta_j^{(s)}, 0, 10)}. \end{align*}\]正規回帰モデルでは$\beta$の事後分散は$\sigma^2(X^TX)^{-1}$と近くなるため、提案分散として$\hat{\sigma}^2(X^TX)^{-1}$(ただし$\hat{\sigma}$は${log(y_1+1/2),\ldots,log(y_n+1/2)}$の標本分散)を用いる
library(mvtnorm)
yX.sparrow <- dget("yX.sparrow.txt")
y <- yX.sparrow[,1]; X <- yX.sparrow[,-1]
n <- length(y); p <- dim(X)[2]
pmn.beta <- rep(0, p)
psd.beta <- rep(10, p)
var.prop <- var(log(y+1/2))*solve(t(X)%*%X)
S <- 10000
beta <- rep(0, p); acs <- 0
BETA <- matrix(0, nrows=S, ncol=p)
set.seed(1)
for(s in 1:S){
beta.p <- t(rmvnorm(1, beta, var.prop))
lhr <- sum(dpois(y, exp(X%*%beta.p), log=T)) -
sum(dpois(y, exp(X%*%beta), log=T)) +
sum(dnorm(beta.p, pmn.beta, psd.beta, log=T)) -
sum(dnorm(beta, pmn.beta, psd.beta, log=T))
if(log(runif(1))<lhr){beta <- beta.p; acs <- acs+1}
BETA[s,] <- beta
}
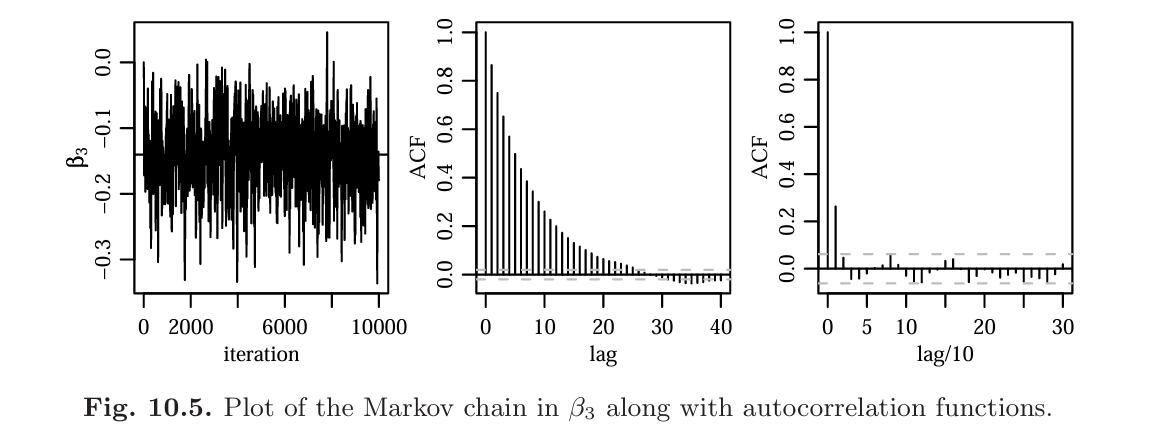
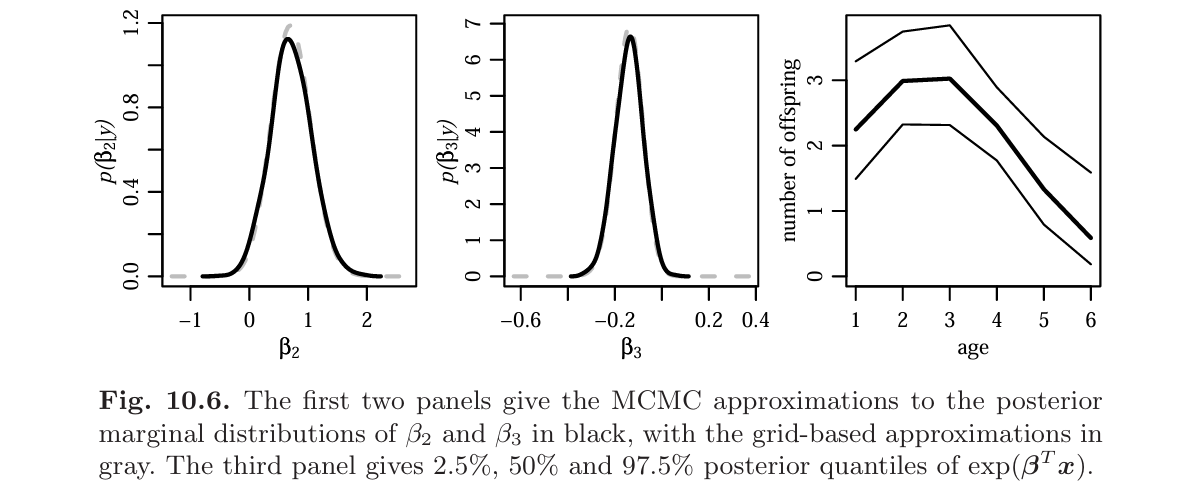
演習問題 10.5
(a)
\[\begin{align*} p(\mathbf{y} \mid \mathbf{x}, \boldsymbol{\beta}, \boldsymbol{\gamma}) &= \prod_{i=1}^{n} \left( \frac{e^{\theta_i}}{1 + e^{\theta_i}} \right)^{y_i} \left( \frac{1}{1 + e^{\theta_i}} \right)^{1 - y_i}\\ \log p(\mathbf{y} \mid \mathbf{x}, \boldsymbol{\beta}, \boldsymbol{\gamma}) &= \sum_{i=1}^{n} \left\{ y_i \log \left( \frac{e^{\theta_i}}{1 + e^{\theta_i}} \right) + (1 - y_i) \log \left( \frac{1}{1 + e^{\theta_i}} \right) \right\}\\ &= \sum_{i=1}^{n} \left\{ y_i [\log(e^{\theta_i}) - \log(1 + e^{\theta_i})] + (1 - y_i) [-\log(1 + e^{\theta_i})] \right\}\\ &= \sum_{i=1}^{n} \left( y_i \theta_i - y_i \log(1 + e^{\theta_i}) - (1 - y_i) \log(1 + e^{\theta_i}) \right)\\ &= \sum_{i=1}^{n} \left( y_i \theta_i - \log(1 + e^{\theta_i}) \right) \end{align*}\] \[\begin{align*} r = \frac{p(\mathbf{y} \mid \mathbf{x}, \boldsymbol{\beta}^{(s)}, \boldsymbol{\gamma}_{-j}^{(s)}, \gamma_j^*) p(\gamma_j^*)} {p(\mathbf{y} \mid \mathbf{x}, \boldsymbol{\beta}^{(s)}, \boldsymbol{\gamma}_{-j}^{(s)}, \gamma_j^{(s)}) p(\gamma_j^{(s)})} \times \frac{J(\gamma_j^{(s)} \mid \gamma_j^*)} {J(\gamma_j^* \mid \gamma_j^{(s)})} \end{align*}\] \[\begin{align*} \beta_j^* \mid \beta_j^{(s)} &\sim \mathcal{N}(\beta_j^{(s)}, \delta^2)\\ \gamma_j^* \mid \gamma_j^{(s)} &= \begin{cases} 0 & \text{if } \gamma_j^{(s)} = 1 \\ 1 & \text{if } \gamma_j^{(s)} = 0 \end{cases} \end{align*}\]library(data.table)
library(dplyr)
library(MASS)
library(coda)
library(ggplot2)
# データ読み込みと整形
data <- fread("azdiabetes.dat", header=TRUE)
col_int <- c("npreg", "glu", "bp", "skin", "age")
col_float <- c("bmi", "ped")
col_str <- "diabetes"
data[ , (col_int) := lapply(.SD, as.integer), .SDcols = col_int]
data[ , (col_float) := lapply(.SD, as.numeric), .SDcols = col_float]
data[ , (col_str) := as.character(get(col_str))]
# デザイン行列と目的変数
predictors <- c("npreg", "bp", "bmi", "ped", "age")
X <- scale(data[ , ..predictors]) %>% as.matrix()
X <- cbind(1, X) # Intercept追加
y <- ifelse(data$diabetes == "Yes", 1, 0)
# 対数尤度関数
log_likelihood <- function(y, X, beta, gamma) {
theta <- X %*% (beta * c(1, gamma))
sum(y * theta - log(1 + exp(theta)))
}
# βの更新
update_beta_j <- function(beta, gamma, j, delta, prior_var) {
beta_prop <- beta
beta_prop[j+1] <- rnorm(1, beta[j+1], delta)
log_lik_diff <- log_likelihood(y, X, beta_prop, gamma) - log_likelihood(y, X, beta, gamma)
log_prior_ratio <- dnorm(beta_prop[j+1], 0, sqrt(prior_var), log=TRUE) -
dnorm(beta[j+1], 0, sqrt(prior_var), log=TRUE)
log_r <- log_lik_diff + log_prior_ratio
if (log(runif(1)) < log_r) return(beta_prop) else return(beta)
}
# γの更新
update_gamma_j <- function(beta, gamma, j) {
gamma_prop <- gamma
gamma_prop[j] <- 1 - gamma_prop[j]
log_r <- log_likelihood(y, X, beta, gamma_prop) - log_likelihood(y, X, beta, gamma)
if (log(runif(1)) < log_r) return(gamma_prop) else return(gamma)
}
# MCMC本体
logit_reg_with_var_select <- function(y, X, beta_init, gamma_init, delta, S=1000, seed=42) {
set.seed(seed)
beta <- beta_init
gamma <- gamma_init
q <- length(beta)
BETA <- matrix(NA, S, q)
GAMMA <- matrix(NA, S, q-1)
for (s in 1:S) {
for (j in 0:(q-1)) {
prior_var <- ifelse(j == 0, 16, 4)
beta <- update_beta_j(beta, gamma, j, delta, prior_var)
}
for (j in 1:(q-1)) {
gamma <- update_gamma_j(beta, gamma, j)
}
BETA[s, ] <- beta
GAMMA[s, ] <- gamma
}
list(BETA = BETA, GAMMA = GAMMA)
}
# 初期値(GLMフィット)
glmfit <- glm(y ~ ., data = as.data.frame(cbind(y, X[,-1])), family = binomial())
beta_init <- coef(glmfit)
gamma_init <- rep(1, 5)
delta <- 0.1
# 実行
res <- logit_reg_with_var_select(y, X, beta_init, gamma_init, delta, S=100000)
# チェーン処理・可視化
chn_beta <- mcmc(res$BETA)
chn_gamma <- mcmc(res$GAMMA)
plot(chn_beta)
plot(chn_gamma)
# β * γ の生成と可視化
beta_gamma_prod <- res$BETA[, -1] * res$GAMMA
beta_times_gamma <- cbind(res$BETA[, 1], beta_gamma_prod)
colnames(beta_times_gamma) <- c("β0", paste0("β", 1:5, "*γ", 1:5))
chn_bg <- mcmc(beta_times_gamma)
plot(chn_bg)
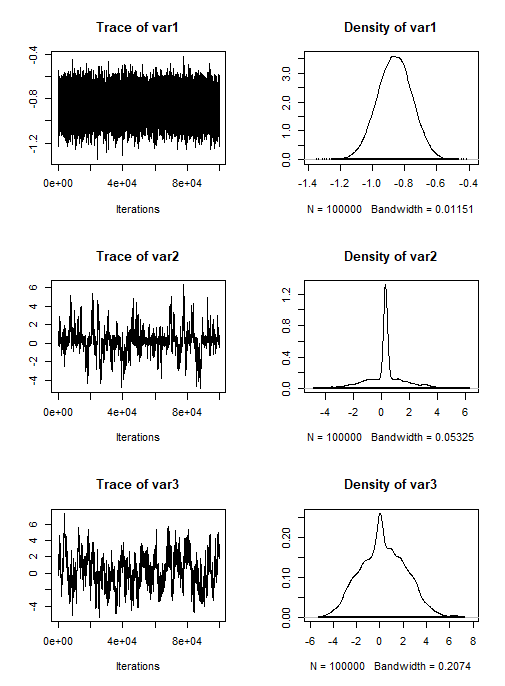
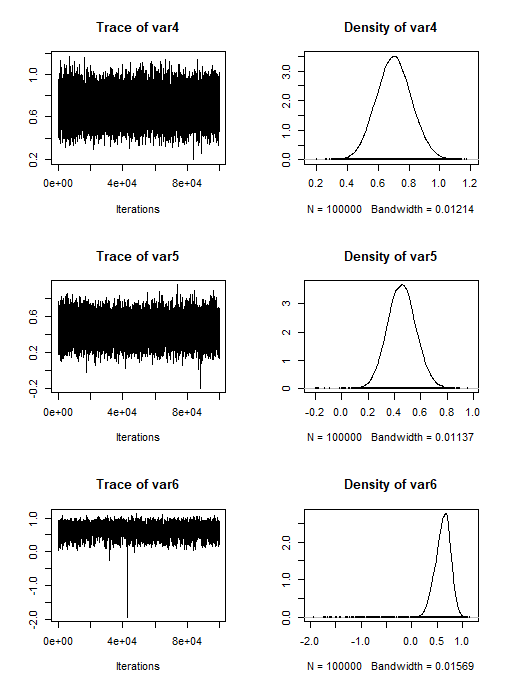
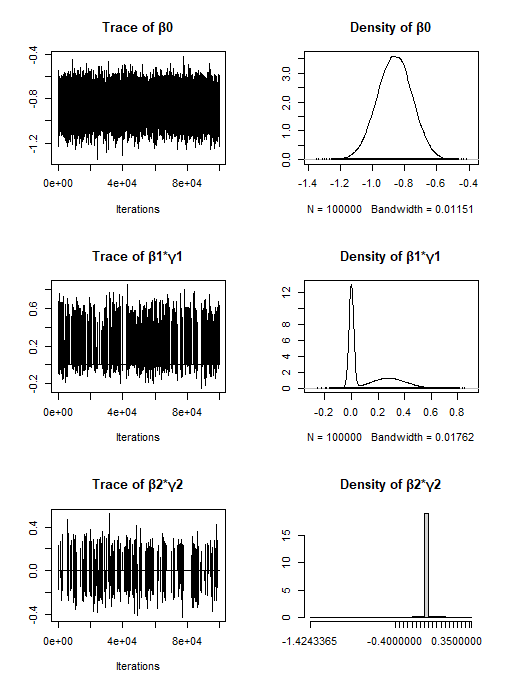
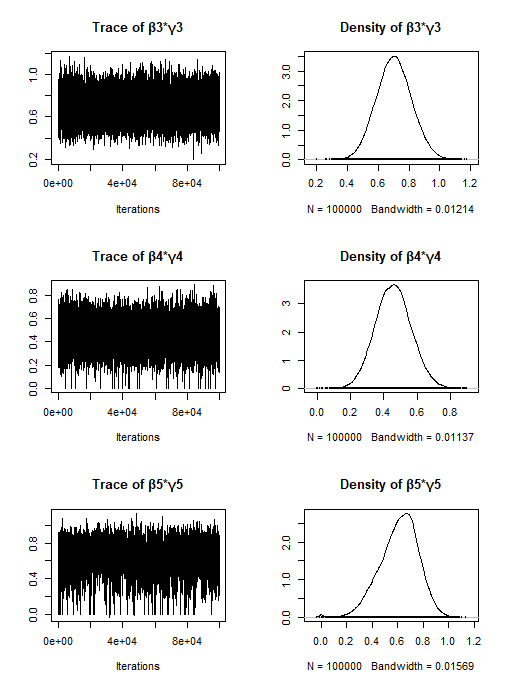
- $\beta$について
- $\beta_1$と$\beta_2$のトレースプロットが横一直線や階段状になっているためミキシングが悪い
- $\beta\times\gamma$について
- 全体的にミキシングが良い
(b)
# γベクトルを文字列(またはベクトル)でリスト化
gamma_tuples <- apply(res$GAMMA, 1, function(row) paste(as.integer(row), collapse = ","))
# 出現回数をカウント
gamma_counts <- table(gamma_tuples)
# 出現回数順にソート(降順)
sorted_gamma_counts <- sort(gamma_counts, decreasing = TRUE)
# 上位5つ
top5_gamma <- head(sorted_gamma_counts, 5)
# 総サンプル数
S <- nrow(res$GAMMA)
# 出力
cat("Top 5 most frequent gamma vectors, counts, and estimated posterior probabilities:\n")
cat("Total samples (S) =", S, "\n")
cat(strrep("-", 60), "\n")
cat("Gamma Vector Count Estimated Probability (Count/S)\n")
cat(strrep("-", 60), "\n")
for (i in seq_along(top5_gamma)) {
gamma_vec <- names(top5_gamma)[i]
count <- as.integer(top5_gamma[i])
prob <- round(count / S, 4)
cat(sprintf("%-18s %-7d %.4f\n", gamma_vec, count, prob))
}
cat(strrep("-", 60), "\n")
Top 5 most frequent gamma vectors, counts, and estimated posterior probabilities:
Total samples (S) = 100000
Gamma Vector Count Estimated Probability (Count/S)
0,0,1,1,1 54127 0.5413
1,0,1,1,1 40473 0.4047
0,1,1,1,1 2852 0.0285
1,1,1,1,1 2264 0.0226
1,0,1,1,0 176 0.0018
- 上位2つのパターンが全体の 約94.6% を占める → ほぼ2モデルに集中している
- $\gamma_3$,$\gamma_4$,$\gamma_5$は上位のモデルで常に1となっており、これらの変数が糖尿病の予測において重要である
- $\gamma_2$は上位のモデルで常に0であり、変数の予測への寄与が小さい
- $\gamma$ベクトルの分布が非常に尖っており、モデル選択の確信度が高いと考えられる
(c)
library(reshape2)
df_bg <- as.data.frame(beta_times_gamma)
df_melted <- melt(df_bg)
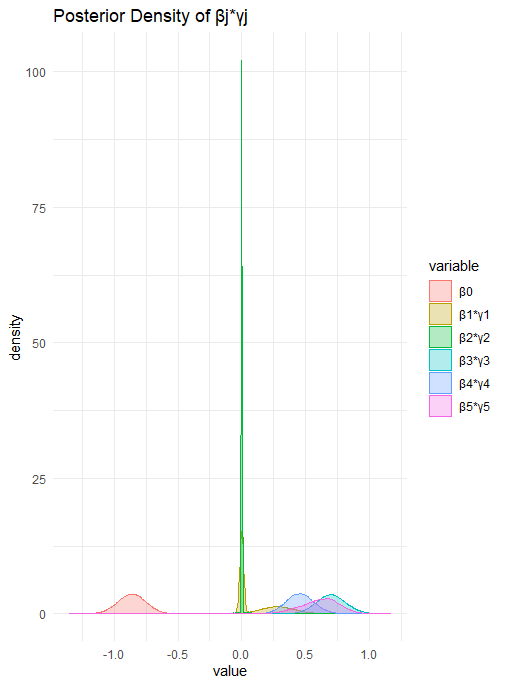
ggplot(df_melted, aes(x = value, color = variable, fill = variable)) +
geom_density(alpha = 0.3) +
labs(title = "Posterior Density of βj*γj") +
theme_minimal()
inclusion_probs <- colMeans(res$GAMMA)
df_inclusion <- data.frame(
Variable = paste0("γ", 1:length(inclusion_probs)),
Inclusion_Probability = round(inclusion_probs, 4)
)
library(knitr)
kable(df_inclusion, caption = "Posterior Inclusion Probabilities")
| Variable | Inclusion_Probability |
|---|---|
| γ1 | 0.4299 |
| γ2 | 0.0519 |
| γ3 | 1.0000 |
| γ4 | 0.9996 |
| γ5 | 0.9975 |