6月19日
演習問題 9.3
(a)
library(MASS) # ginv など
library(mvtnorm) # 多変量正規分布からのサンプリング
library(readr) # read_delim
library(dplyr) # データフレーム操作
library(tibble)
# データ読み込み
df <- read_table("crime.dat", col_names = TRUE)
# 説明変数と目的変数に分割
y <- df$y
X <- df %>% select(-y) %>% as.matrix()
X <- cbind(1, X) # 切片を追加
n <- nrow(X)
p <- ncol(X)
# 最小二乗による残差分散推定
ResidualSE <- function(y, X) {
fit <- lm(y ~ X - 1) # X には既に切片があるので -1
rss <- sum(resid(fit)^2)
return(rss / (n - p))
}
# g-prior によるベイズ回帰サンプリング
lmGprior <- function(y, X, g = n, nu0 = 1, sigma0_sq = ResidualSE(y, X), S = 1000) {
XtX_inv <- ginv(t(X) %*% X)
Hg <- (g / (g + 1)) * X %*% XtX_inv %*% t(X)
SSRg <- t(y) %*% (diag(n) - Hg) %*% y
sigma_sq_samples <- 1 / rgamma(S, shape = (nu0 + n) / 2, rate = (nu0 * sigma0_sq + SSRg) / 2)
Vb <- g / (g + 1) * XtX_inv
Eb <- Vb %*% t(X) %*% y
beta_samples <- matrix(0, nrow = S, ncol = p)
for (i in 1:S) {
s <- sigma_sq_samples[i]
beta_samples[i, ] <- rmvnorm(1, mean = as.vector(Eb), sigma = s * Vb)
}
list(beta = beta_samples, sigma_sq = sigma_sq_samples)
}
# パラメータ設定と実行
g <- n
nu0 <- 2
sigma0_sq <- 1
S <- 5000
res <- lmGprior(y, X, g, nu0, sigma0_sq, S)
beta_samples <- res$beta
# 事後平均と信用区間
beta_mean <- colMeans(beta_samples)
ci <- apply(beta_samples, 2, quantile, probs = c(0.025, 0.975))
# 結果をデータフレームにまとめる
param_names <- c("intercept", colnames(df)[colnames(df) != "y"])
result <- tibble(
param = param_names,
beta_hat = beta_mean,
ci_lower = ci[1, ],
ci_upper = ci[2, ],
ci_length = ci[2, ] - ci[1, ]
)
print(result)
# A tibble: 16 × 5
param beta_hat ci_lower ci_upper ci_length
<chr> <dbl> <dbl> <dbl> <dbl>
1 intercept -0.000194 -0.141 0.142 0.283
2 M 0.281 0.0320 0.532 0.500
3 So -0.00311 -0.325 0.331 0.657
4 Ed 0.534 0.224 0.859 0.636
5 Po1 1.43 -0.0351 2.91 2.94
6 Po2 -0.760 -2.27 0.779 3.05
7 LF -0.0657 -0.347 0.213 0.560
8 M.F 0.133 -0.147 0.409 0.555
9 Pop -0.0675 -0.298 0.160 0.458
10 NW 0.108 -0.189 0.420 0.609
11 U1 -0.269 -0.626 0.0901 0.717
12 U2 0.363 0.0471 0.683 0.636
13 GDP 0.236 -0.228 0.709 0.937
14 Ineq 0.715 0.289 1.14 0.856
15 Prob -0.278 -0.520 -0.0270 0.493
16 Time -0.0597 -0.299 0.180 0.479
# OLS(最小二乗法)回帰モデル
olsfit <- lm(y ~ X - 1) # Xには切片が含まれているので -1 を指定
# 回帰係数の要約統計量を抽出
summary_fit <- summary(olsfit)
coef_summary <- summary_fit$coefficients
# 名前の取得(同じく X に切片が入っている前提)
coef_name <- c("intercept", colnames(df)[colnames(df) != "y"])
# 信頼区間(デフォルトで95%)
ci <- confint(olsfit)
# 結果をデータフレームにまとめる
result_ols <- tibble(
param = coef_name,
beta_hat = coef_summary[, "Estimate"],
pvalue = coef_summary[, "Pr(>|t|)"],
ci_lower = ci[, 1],
ci_upper = ci[, 2],
ci_length = ci[, 2] - ci[, 1]
)
print(result_ols)
# A tibble: 16 × 6
param beta_hat pvalue ci_lower ci_upper ci_length
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 intercept -0.000458 0.995 -0.161 0.161 0.322
2 M 0.287 0.0430 0.00956 0.563 0.554
3 So -0.000114 1.00 -0.375 0.375 0.751
4 Ed 0.545 0.00488 0.178 0.911 0.733
5 Po1 1.47 0.0813 -0.194 3.14 3.33
6 Po2 -0.782 0.366 -2.52 0.955 3.47
7 LF -0.0660 0.670 -0.379 0.247 0.626
8 M.F 0.131 0.404 -0.185 0.448 0.633
9 Pop -0.0703 0.584 -0.329 0.189 0.518
10 NW 0.109 0.531 -0.242 0.460 0.701
11 U1 -0.271 0.179 -0.672 0.130 0.802
12 U2 0.369 0.0489 0.00191 0.736 0.734
13 GDP 0.238 0.365 -0.290 0.766 1.06
14 Ineq 0.726 0.00408 0.249 1.20 0.955
15 Prob -0.285 0.0410 -0.558 -0.0124 0.546
16 Time -0.0616 0.642 -0.329 0.206 0.534
95%信用区間/信頼区間の長さについて、ベイズ回帰の方が最小二乗推定よりも短い。また、ベイズ回帰の結果を見ると、M、Ed、U2、Ineqの係数の95%信用区間には0が含まれていないため、これらの変数は犯罪率の強い予測因子であると考えられる一方、最小二乗推定の結果では、M、Ed、U2、Ineq、Probのp値が0.05未満であるため、これらの変数が犯罪率の強い予測因子であると考えられる。
(b)
set.seed(1234) # 乱数シード固定
n <- nrow(X) # 全データ数
i_te <- sample(1:n, n %/% 2, replace = FALSE) # テスト用インデックス
i_tr <- setdiff(1:n, i_te) # 学習用インデックス
# データ分割
X_tr <- X[i_tr, , drop = FALSE]
X_te <- X[i_te, , drop = FALSE]
y_tr <- y[i_tr]
y_te <- y[i_te]
# OLSモデル学習
olsfit <- lm(y_tr ~ X_tr - 1) # X_tr に切片が含まれている前提なので -1
# 係数取得 → 予測 → MSE計算
beta_hat <- coef(olsfit)
y_hat <- X_te %*% beta_hat
error_ols <- mean((y_te - y_hat)^2)
print(error_ols)
library(ggplot2)
df_plot <- data.frame(
Actual = y_te,
Predicted = as.vector(y_hat)
)
# 散布図 + 対角線(理想線)
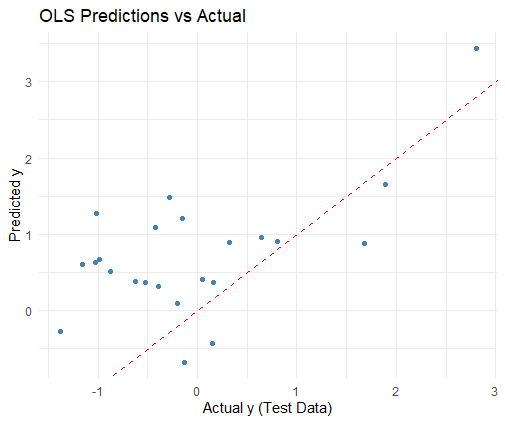
ggplot(df_plot, aes(x = Actual, y = Predicted)) +
geom_point(color = "steelblue") +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
labs(title = "OLS Predictions vs Actual",
x = "Actual y (Test Data)",
y = "Predicted y") +
theme_minimal()
[1] 1.261635
# ベイズ回帰のサンプリング
g <- nrow(X_tr)
bayes_fit <- lmGprior(y_tr, X_tr, g, nu0, sigma0_sq, S)
# 事後平均の回帰係数
beta_hat_bayes <- colMeans(bayes_fit$BETA)
# テストデータで予測
y_hat_bayes <- X_te %*% beta_hat_bayes
# 平均二乗誤差 (MSE)
error_bayes <- mean((y_te - y_hat_bayes)^2)
print(error_bayes)
df_bayes_plot <- data.frame(
Actual = y_te,
Predicted = as.vector(y_hat_bayes)
)
ggplot(df_bayes_plot, aes(x = Actual, y = Predicted)) +
geom_point(color = "darkgreen") +
geom_abline(intercept = 0, slope = 1, color = "red", linetype = "dashed") +
labs(title = "Bayesian Regression Predictions vs Actual",
x = "Actual y (Test Data)",
y = "Predicted y") +
theme_minimal()
[1] 1.2272
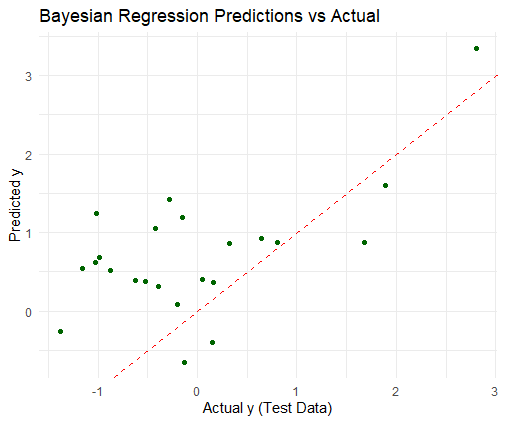
最小二乗法とベイズ法は、テスト・データについて非常によく似た予測をもたらすように見える。今回、ベイズ法は最小二乗法よりも精度が高いが、その差はとても小さい。
(c)
# データ分割関数
splitData <- function(y, X) {
n <- nrow(X)
i_te <- sample(1:n, n %/% 2, replace = FALSE)
i_tr <- setdiff(1:n, i_te)
list(
y_tr = y[i_tr],
y_te = y[i_te],
X_tr = X[i_tr, , drop = FALSE],
X_te = X[i_te, , drop = FALSE]
)
}
# 残差分散推定
ResidualSE <- function(y, X) {
n <- nrow(X)
p <- ncol(X)
fit <- lm(y ~ X - 1)
rss <- sum(resid(fit)^2)
rss / (n - p)
}
# MSEを計算する関数
computeMses <- function(y, X, g, nu0, sigma0_sq, S) {
split <- splitData(y, X)
y_tr <- split$y_tr
y_te <- split$y_te
X_tr <- split$X_tr
X_te <- split$X_te
# OLS
ols_fit <- lm(y_tr ~ X_tr - 1)
beta_hat_ols <- coef(ols_fit)
y_hat_ols <- X_te %*% beta_hat_ols
error_ols <- mean((y_te - y_hat_ols)^2)
# Bayesian
bayes_fit <- lmGprior(y_tr, X_tr, g, nu0, sigma0_sq, S)
beta_hat_bayes <- colMeans(bayes_fit$beta)
y_hat_bayes <- X_te %*% beta_hat_bayes
error_bayes <- mean((y_te - y_hat_bayes)^2)
c(error_ols = error_ols, error_bayes = error_bayes)
}
# 実行設定
set.seed(1234)
n_sim <- 1000
error_ols <- numeric(n_sim)
error_bayes <- numeric(n_sim)
g <- nrow(X)
n <- nrow(X)
# シミュレーション
for (i in 1:n_sim) {
errors <- computeMses(y, X, g, nu0, sigma0_sq, S)
error_ols[i] <- errors["error_ols"]
error_bayes[i] <- errors["error_bayes"]
}
# 平均MSEの表示
cat("平均OLS MSE: ", mean(error_ols), "\n")
cat("平均Bayesian MSE: ", mean(error_bayes), "\n")
> cat("平均OLS MSE: ", mean(error_ols), "\n")
平均OLS MSE: 0.1485031
> cat("平均Bayesian MSE: ", mean(error_bayes), "\n")
平均Bayesian MSE: 0.1407067